llama3源码解析-03：model.py模块解析

Last updated on December 30, 2024 am

llama

整体

model.py 模块是 Llama 3 模型的核心实现部分，主要负责定义和实现 Transformer 模型的结构及其相关组件。

1. 模型参数定义 (`ModelArgs` 类)

ModelArgs 类是一个数据类，用于定义和存储模型的各种超参数，例如：
- dim: 模型的维度。
- n_layers: Transformer 的层数。
- n_heads: 注意力机制中的头数。
- vocab_size: 词汇表大小。
- max_batch_size: 最大批处理大小。
- max_seq_len: 最大序列长度。
这些参数在模型初始化时被使用，决定了模型的结构和行为。

2. RMSNorm 层 (`RMSNorm` 类)

RMSNorm 是一个自定义的归一化层，用于替代传统的 LayerNorm。它通过对输入进行均方根归一化来稳定训练过程。
该层在 Transformer 的每个子层（如注意力机制和前馈网络）之后使用。

3. RoPE (Rotary Positional Embedding)

该模块实现了旋转位置编码（RoPE），用于为输入序列中的每个位置生成位置编码。RoPE 通过将位置信息嵌入到注意力机制中，帮助模型捕捉序列中的位置关系。
precompute_freqs_cis 函数预计算了频率矩阵，apply_rotary_emb 函数将旋转位置编码应用到查询和键向量上。

4. 注意力机制 (`Attention` 类)

Attention 类实现了多头注意力机制（Multi-Head Attention），这是 Transformer 模型的核心组件之一。
它使用 ColumnParallelLinear 和 RowParallelLinear 来实现并行的线性变换，支持模型并行化。
该模块还实现了键值缓存（KV Cache），用于在生成过程中缓存先前的键和值，以减少重复计算。

5. 前馈网络 (`FeedForward` 类)

FeedForward 类实现了 Transformer 中的前馈神经网络（FFN），通常由两个线性变换和一个激活函数（如 SiLU）组成。
该模块也支持模型并行化，使用 ColumnParallelLinear 和 RowParallelLinear 来实现并行的线性变换。

6. Transformer 块 (`TransformerBlock` 类)

TransformerBlock 类将注意力机制和前馈网络组合在一起，形成一个完整的 Transformer 层。
每个 Transformer 块包含一个注意力层和一个前馈网络层，并且在每个子层之后应用 RMSNorm 进行归一化。

7. Transformer 模型 (`Transformer` 类)

Transformer 类是整个模型的核心，它由多个 TransformerBlock 组成，形成一个深层的 Transformer 网络。
该模块还负责处理输入嵌入、位置编码、以及最终的输出线性变换。
forward 方法实现了模型的前向传播过程，包括嵌入、位置编码、多层 Transformer 块的处理以及最终的输出生成。

8. 模型并行化

该模块使用了 fairscale 库中的 ColumnParallelLinear 和 RowParallelLinear 来实现模型并行化，允许模型在多个 GPU 上分布计算，从而提高训练和推理的效率。

9. 推理模式

在推理模式下，模型使用 torch.inference_mode() 来禁用梯度计算，从而提高推理速度并减少内存占用。

总结：

model.py 模块定义了 Llama 3 模型的核心架构，包括 Transformer 的各个组件（如注意力机制、前馈网络、归一化层等），并实现了模型并行化和推理优化。它是整个 Llama 3 模型的基础，负责处理输入数据并生成输出。

模型详细流程图

graph TD
    A[输入 tokens] --> B[Token Embedding]
    B --> C[添加位置编码 freqs_cis]
    C --> D[初始化 mask]
    D --> E[进入 Transformer 层]
    E --> F[Transformer Block 1]
    E --> G[Transformer Block 2]
    E --> H[...]
    E --> I[Transformer Block N]
    F --> J[输出 logits]
    G --> J
    H --> J
    I --> J

    subgraph Transformer Block
        direction TB
        K[输入] --> L[RMSNorm]
        L --> M[Attention]
        M --> N[Add & Norm]
        N --> O[FeedForward]
        O --> P[Add & Norm]
        P --> Q[输出]
    end

    F --> K
    G --> K
    I --> K

输入 tokens
- 输入是一个批次的 token IDs，形状为 (batch_size, seq_len)。
Token Embedding
- 通过 tok_embeddings 将 token IDs 转换为嵌入向量，形状为 (batch_size, seq_len, dim)。
添加位置编码 freqs_cis
- 使用预计算的 freqs_cis 为嵌入向量添加旋转位置编码，帮助模型捕捉序列中的位置信息。
初始化 mask
- 根据 seq_len 和 start_pos 生成注意力掩码 mask，用于防止模型看到未来的 token。
进入 Transformer 层
- 嵌入向量和位置编码进入多层 Transformer 块进行处理。
Transformer Block 1 到 N
- 每个 Transformer 块包含以下步骤：
  - RMSNorm: 对输入进行归一化。
  - Attention: 应用多头注意力机制，生成注意力输出。
  - RMSNorm: 对注意力输出进行归一化。
  - FeedForward: 应用前馈网络，生成最终的 Transformer 块输出。
应用 RMSNorm
- 在所有 Transformer 块处理完成后，对最终输出应用 RMSNorm 进行归一化。
输出线性变换
- 通过 output 线性层将归一化后的输出映射到词汇表空间，形状为 (batch_size, seq_len, vocab_size)。
输出 logits
- 返回最终的 logits，表示每个 token 的概率分布。

`class ModelArgs`

@dataclass
class ModelArgs:
    dim: int = 4096  # 模型的维度，即每个token的向量表示的大小
    n_layers: int = 32  # 模型的层数，即Transformer的层数
    n_heads: int = 32  # 注意力机制中的头数
    n_kv_heads: Optional[int] = None  # 键值头的数量，如果为None，则与n_heads相同
    vocab_size: int = -1  # 词汇表的大小，通常由tokenizer决定
    multiple_of: int = 256  # SwiGLU激活函数中隐藏层大小的倍数，确保是256的倍数
    ffn_dim_multiplier: Optional[float] = None  # 前馈网络维度的乘数，用于调整隐藏层大小
    norm_eps: float = 1e-5  # Layer Normalization中的epsilon值，用于数值稳定性
    rope_theta: float = 500000  # RoPE（Rotary Position Embedding）中的theta参数

    max_batch_size: int = 32  # 最大批处理大小
    max_seq_len: int = 2048  # 最大序列长度

`class RMSNorm`

class RMSNorm(torch.nn.Module):
    def __init__(self, dim: int, eps: float = 1e-6):
        super().__init__()
        self.eps = eps  # 用于数值稳定性的小值，防止除以零
        self.weight = nn.Parameter(torch.ones(dim))  # 可学习的缩放参数，初始化为1

    def _norm(self, x):
        # 计算RMS（Root Mean Square）归一化，对输入x进行归一化处理
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x):
        # 前向传播函数，先对输入x进行归一化，然后乘以可学习的缩放参数
        output = self._norm(x.float()).type_as(x)  # 归一化并保持与输入x相同的数据类型
        return output * self.weight  # 乘以缩放参数

解释：

ModelArgs:
- 这是一个数据类，用于存储模型的配置参数。它定义了模型的结构和超参数，如模型的维度、层数、注意力头数等。
- dim 是每个token的向量表示的大小，n_layers 是Transformer的层数，n_heads 是注意力机制中的头数。
- vocab_size 是词汇表的大小，通常由tokenizer决定。
- multiple_of 和 ffn_dim_multiplier 用于调整前馈网络的隐藏层大小。
- norm_eps 是Layer Normalization中的epsilon值，用于数值稳定性。
- rope_theta 是RoPE（Rotary Position Embedding）中的theta参数，用于位置编码。
- max_batch_size 和 max_seq_len 分别定义了模型的最大批处理大小和最大序列长度。
RMSNorm:
- 这是一个自定义的归一化层，类似于Layer Normalization，但使用了RMS（Root Mean Square）归一化。
- _norm 方法计算输入的RMS归一化值，forward 方法在前向传播时对输入进行归一化并乘以可学习的缩放参数。
- eps 是一个小值，用于防止除以零的情况，weight 是可学习的缩放参数，初始化为1。

这两个类在模型中分别用于定义模型的结构和实现归一化操作，是Transformer模型的重要组成部分。

旋转位置编码

`precompute_freqs_cis`

def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    """
    预计算旋转位置编码的频率矩阵 (freqs_cis)。

    旋转位置编码 (Rotary Positional Embedding, RoPE) 是一种将位置信息嵌入到注意力机制中的方法。
    它通过将位置信息编码为复数形式，应用到查询和键向量上。

    参数:
        dim (int): 模型的维度（通常是注意力头的维度）。
        end (int): 序列的最大长度。
        theta (float): 控制频率的基数，默认为 10000.0。

    返回:
        freqs_cis (torch.Tensor): 预计算的频率矩阵，形状为 (end, dim // 2)，数据类型为 complex64。
    """
    # 计算频率向量
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # 生成位置向量
    t = torch.arange(end, device=freqs.device, dtype=torch.float32)
    # 计算外积，得到频率矩阵
    freqs = torch.outer(t, freqs)
    # 将频率矩阵转换为复数形式（极坐标表示）
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis

解释：

作用: 预计算旋转位置编码的频率矩阵 freqs_cis，用于将位置信息嵌入到查询和键向量中。
输入:
- dim: 模型的维度，通常是注意力头的维度。
- end: 序列的最大长度。
- theta: 控制频率的基数，默认为 10000.0。
输出:
- freqs_cis: 预计算的频率矩阵，形状为 (end, dim // 2)，数据类型为 complex64。
关键点:
- 使用 torch.outer 计算位置向量和频率向量的外积，得到频率矩阵。
- 通过 torch.polar 将频率矩阵转换为复数形式，表示极坐标。

`reshape_for_broadcast`

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    """
    将频率矩阵 `freqs_cis` 重塑为适合广播的形状，以便与查询或键向量进行逐元素操作。

    参数:
        freqs_cis (torch.Tensor): 频率矩阵，形状为 (seq_len, dim // 2)。
        x (torch.Tensor): 查询或键向量，形状为 (batch_size, seq_len, n_heads, head_dim)。

    返回:
        freqs_cis (torch.Tensor): 重塑后的频率矩阵，形状为 (1, seq_len, 1, dim // 2)。
    """
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    # 重塑频率矩阵，使其形状为 (1, seq_len, 1, dim // 2)
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)

解释：

作用: 将频率矩阵 freqs_cis 重塑为适合广播的形状，以便与查询或键向量进行逐元素操作。
输入:
- freqs_cis: 频率矩阵，形状为 (seq_len, dim // 2)。
- x: 查询或键向量，形状为 (batch_size, seq_len, n_heads, head_dim)。
输出:
- 重塑后的频率矩阵，形状为 (1, seq_len, 1, dim // 2)。
关键点:
- 通过 view 方法将频率矩阵重塑为适合广播的形状，使其能够与查询或键向量进行逐元素操作。

`apply_rotary_emb`

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    """
    将旋转位置编码应用到查询和键向量上。

    旋转位置编码通过将位置信息嵌入到查询和键向量中，帮助模型捕捉序列中的位置关系。

    参数:
        xq (torch.Tensor): 查询向量，形状为 (batch_size, seq_len, n_heads, head_dim)。
        xk (torch.Tensor): 键向量，形状为 (batch_size, seq_len, n_heads, head_dim)。
        freqs_cis (torch.Tensor): 频率矩阵，形状为 (1, seq_len, 1, head_dim // 2)。

    返回:
        xq_out (torch.Tensor): 应用旋转位置编码后的查询向量。
        xk_out (torch.Tensor): 应用旋转位置编码后的键向量。
    """
    # 将查询和键向量转换为复数形式
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    # 重塑频率矩阵以匹配查询和键向量的形状
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    # 应用旋转位置编码
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

解释：

作用: 将旋转位置编码应用到查询和键向量上，帮助模型捕捉序列中的位置关系。
输入:
- xq: 查询向量，形状为 (batch_size, seq_len, n_heads, head_dim)。
- xk: 键向量，形状为 (batch_size, seq_len, n_heads, head_dim)。
- freqs_cis: 频率矩阵，形状为 (1, seq_len, 1, head_dim // 2)。
输出:
- xq_out: 应用旋转位置编码后的查询向量。
- xk_out: 应用旋转位置编码后的键向量。
关键点:
- 使用 torch.view_as_complex 将查询和键向量转换为复数形式。
- 通过逐元素乘法将频率矩阵应用到查询和键向量上。
- 使用 torch.view_as_real 将结果转换回实数形式。
这些函数共同实现了旋转位置编码（RoPE）

总结：
- precompute_freqs_cis: 预计算旋转位置编码的频率矩阵。
- reshape_for_broadcast: 将频率矩阵重塑为适合广播的形状。
- apply_rotary_emb: 将旋转位置编码应用到查询和键向量上。

`repeat_kv`

def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """
    重复键或值向量，以匹配查询向量的头数。

    在分组注意力机制中，键和值向量的头数可能少于查询向量的头数，因此需要重复键和值向量以匹配查询向量的头数。

    参数:
        x (torch.Tensor): 键或值向量，形状为 (batch_size, seq_len, n_kv_heads, head_dim)。
        n_rep (int): 重复次数，通常为查询头数与键值头数的比值。

    返回:
        torch.Tensor: 重复后的键或值向量，形状为 (batch_size, seq_len, n_kv_heads * n_rep, head_dim)。
    """
    bs, slen, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    return (
        x[:, :, :, None, :]
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )

解释：

作用: 重复键或值向量，以匹配查询向量的头数。
输入:
- x: 键或值向量，形状为 (batch_size, seq_len, n_kv_heads, head_dim)。
- n_rep: 重复次数，通常为查询头数与键值头数的比值。
输出:
- 重复后的键或值向量，形状为 (batch_size, seq_len, n_kv_heads * n_rep, head_dim)。
关键点:
- 使用 expand 和 reshape 方法重复键或值向量，使其头数与查询向量匹配。

`class Attention`

class Attention 实现了 Transformer 中的 多头注意力机制（Multi-Head Attention），它是 Transformer 模型的核心组件之一。以下是该类的详细解释：

主要功能：

多头注意力机制：
- 将输入向量拆分为多个头，每个头独立计算注意力分数。
- 通过并行计算，捕捉输入序列中不同位置之间的关系。
键值缓存（KV Cache）：
- 在生成任务中，缓存先前的键和值，避免重复计算，提高效率。
模型并行化：
- 使用 ColumnParallelLinear 和 RowParallelLinear 实现并行的线性变换，支持多 GPU 计算。

关键组件：

线性变换：
- wq、wk、wv：分别对输入进行线性变换，生成查询（Query）、键（Key）和值（Value）向量。
- wo：将多头注意力的输出进行线性变换，合并为最终输出。
键值缓存：
- cache_k 和 cache_v：用于缓存先前的键和值，形状为 (batch_size, max_seq_len, n_local_kv_heads, head_dim)。
旋转位置编码（RoPE）：
- 通过 apply_rotary_emb 将位置信息嵌入到查询和键向量中。
注意力分数计算：
- 计算查询和键的点积，除以 sqrt(head_dim) 进行缩放，然后应用 Softmax 得到注意力分数。
输出计算：
- 使用注意力分数对值向量进行加权求和，得到多头注意力的输出。

`流程图

graph TD
    A[输入 x] --> B[线性变换]
    B --> C[生成 Query]
    B --> D[生成 Key]
    B --> E[生成 Value]
    C --> F[应用旋转位置编码]
    D --> F
    F --> G[更新键值缓存]
    G --> H[计算注意力分数]
    H --> I[应用 Softmax]
    I --> J[加权求和]
    J --> K[线性变换]
    K --> L[输出]

详细步骤说明：

输入 x
- 输入是一个批次的嵌入向量，形状为 (batch_size, seq_len, dim)。
线性变换
- 通过 wq、wk、wv 分别对输入进行线性变换，生成查询（Query）、键（Key）和值（Value）向量。
生成 Query、Key、Value
- 查询向量形状为 (batch_size, seq_len, n_local_heads, head_dim)。
- 键和值向量形状为 (batch_size, seq_len, n_local_kv_heads, head_dim)。
应用旋转位置编码
- 使用 apply_rotary_emb 将旋转位置编码应用到查询和键向量上。
更新键值缓存
- 将当前的键和值向量缓存到 cache_k 和 cache_v 中。
计算注意力分数
- 计算查询和键的点积，除以 sqrt(head_dim) 进行缩放，得到注意力分数。
应用 Softmax
- 对注意力分数应用 Softmax，得到归一化的注意力权重。
加权求和
- 使用注意力权重对值向量进行加权求和，得到多头注意力的输出。
线性变换
- 通过 wo 对多头注意力的输出进行线性变换，合并为最终输出。
输出
- 返回最终的输出，形状为 (batch_size, seq_len, dim)。

代码实现的关键点：

并行化：
- 使用 ColumnParallelLinear 和 RowParallelLinear 实现并行的线性变换，支持多 GPU 计算。
键值缓存：
- 在生成任务中，缓存先前的键和值，避免重复计算，提高效率。
旋转位置编码：
- 通过 apply_rotary_emb 将位置信息嵌入到查询和键向量中，帮助模型捕捉序列中的位置关系。
注意力分数计算：
- 使用点积计算注意力分数，并通过 Softmax 进行归一化。
输出计算：
- 使用注意力权重对值向量进行加权求和，得到多头注意力的输出。

总结：

class Attention 实现了 Transformer 中的多头注意力机制，通过并行化、键值缓存和旋转位置编码等技术，高效地捕捉输入序列中的关系。

`FeedForward`

graph TD
    A[输入 x] --> B[线性变换 W1]
    B --> C[激活函数 SiLU]
    C --> D[线性变换 W3]
    D --> E[逐元素乘法]
    E --> F[线性变换 W2]
    F --> G[输出]

详细步骤说明：

输入 x
- 输入是一个批次的向量，形状为 (batch_size, seq_len, dim)。
线性变换 W1
- 通过 w1 对输入进行线性变换，生成中间向量，形状为 (batch_size, seq_len, hidden_dim)。
激活函数 SiLU
- 对线性变换后的结果应用 SiLU（Sigmoid Linear Unit）激活函数，公式为：
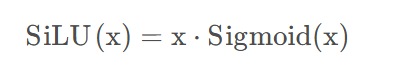
线性变换 W3
- 通过 w3 对输入进行另一个线性变换，生成中间向量，形状为 (batch_size, seq_len, hidden_dim)。
逐元素乘法
- 将 SiLU(W1(x)) 和 W3(x) 进行逐元素乘法，生成加权后的中间向量。
线性变换 W2
- 通过 w2 对加权后的中间向量进行线性变换，生成最终输出，形状为 (batch_size, seq_len, dim)。
输出
- 返回最终的输出，作为前馈网络的结果。

代码实现的关键点：

并行化：
- 使用 ColumnParallelLinear 和 RowParallelLinear 实现并行的线性变换，支持多 GPU 计算。
激活函数：
- 使用 SiLU 激活函数，结合了 Sigmoid 和线性变换的优点，增强了模型的非线性表达能力。
逐元素乘法：
- 将两个线性变换的结果进行逐元素乘法，生成加权后的中间向量。
输出计算：
- 通过 w2 对加权后的中间向量进行线性变换，生成最终输出。

总结：

FeedForward 类实现了 Transformer 中的前馈网络，通过线性变换、激活函数和逐元素乘法等技术，增强了模型的非线性表达能力。

`TransformerBlock`

graph TD
    A[输入 x] --> B[RMSNorm]
    B --> C[Attention]
    C --> D[Add & Norm]
    D --> E[FeedForward]
    E --> F[Add & Norm]
    F --> G[输出]

详细步骤说明：

输入 x
- 输入是一个批次的向量，形状为 (batch_size, seq_len, dim)。
RMSNorm
- 对输入进行 RMSNorm 归一化，公式为：
  [
  \text{RMSNorm}(x) = \frac{x}{\sqrt{\text{mean}(x^2) + \epsilon}} \cdot \gamma
  ]
  其中，(\gamma) 是可学习的缩放参数，(\epsilon) 是防止除零的小常数。
Attention
- 将归一化后的输入传递给 Attention 模块，计算多头注意力机制的输出。
Add & Norm
- 将注意力输出与输入进行残差连接，然后再次应用 RMSNorm 归一化。
FeedForward
- 将归一化后的结果传递给 FeedForward 模块，计算前馈网络的输出。
Add & Norm
- 将前馈网络输出与上一层的输出进行残差连接，然后再次应用 RMSNorm 归一化。
输出
- 返回最终的输出，作为 Transformer 块的结果。

代码实现的关键点：

残差连接：
- 在注意力机制和前馈网络之后，分别使用残差连接，将输入与输出相加，缓解梯度消失问题。
归一化：
- 使用 RMSNorm 对输入和输出进行归一化，稳定训练过程。
注意力机制：
- 通过 Attention 模块计算多头注意力机制的输出，捕捉输入序列中的关系。
前馈网络：
- 通过 FeedForward 模块增强模型的非线性表达能力。

总结：

TransformerBlock 类实现了 Transformer 中的一个完整块，包括注意力机制、前馈网络、残差连接和归一化操作。

`class Transformer`

graph TD
    A[输入 tokens] --> B[Token Embedding]
    B --> C[添加位置编码 freqs_cis]
    C --> D[初始化 mask]
    D --> E[进入 Transformer 层]
    E --> F[Transformer Block 1]
    E --> G[Transformer Block 2]
    E --> H[...]
    E --> I[Transformer Block N]
    F --> J[RMSNorm]
    G --> J
    H --> J
    I --> J
    J --> K[输出线性变换]
    K --> L[输出 logits]

    subgraph Transformer Block
        direction TB
        M[输入] --> N[RMSNorm]
        N --> O[Attention]
        O --> P[Add & Norm]
        P --> Q[FeedForward]
        Q --> R[Add & Norm]
        R --> S[输出]
    end

    F --> M
    G --> M
    I --> M

详细步骤说明：

整体流程：

输入 tokens
- 输入是一个批次的 token IDs，形状为 (batch_size, seq_len)。
Token Embedding
- 通过 tok_embeddings 将 token IDs 转换为嵌入向量，形状为 (batch_size, seq_len, dim)。
添加位置编码 freqs_cis
- 使用预计算的 freqs_cis 为嵌入向量添加旋转位置编码，帮助模型捕捉序列中的位置信息。
初始化 mask
- 根据 seq_len 和 start_pos 生成注意力掩码 mask，用于防止模型看到未来的 token。
进入 Transformer 层
- 嵌入向量和位置编码进入多层 Transformer 块进行处理。
Transformer Block 1 到 N
- 每个 Transformer 块内部执行子图中的流程。
RMSNorm
- 在所有 Transformer 块处理完成后，对最终输出应用 RMSNorm 进行归一化。
输出线性变换
- 通过 output 线性层将归一化后的输出映射到词汇表空间，形状为 (batch_size, seq_len, vocab_size)。
输出 logits
- 返回最终的 logits，表示每个 token 的概率分布。

Transformer Block 子流程：

输入
- 接收来自上一层的输入。
RMSNorm
- 对输入进行归一化。
Attention
- 应用多头注意力机制，生成注意力输出。
Add & Norm
- 将注意力输出与输入进行残差连接，并再次应用 RMSNorm 进行归一化。
FeedForward
- 应用前馈网络，生成前馈输出。
Add & Norm
- 将前馈输出与上一层的输出进行残差连接，并再次应用 RMSNorm 进行归一化。
输出
- 返回当前 Transformer 块的输出，作为下一层的输入。

代码实现的关键点：

嵌入和位置编码：
- 使用 tok_embeddings 将 token IDs 转换为嵌入向量，并通过 freqs_cis 添加位置信息。
注意力掩码：
- 生成注意力掩码 mask，防止模型看到未来的 token。
多层 Transformer 块：
- 通过多个 Transformer 块处理输入，每个块包含注意力机制、前馈网络、残差连接和归一化操作。
输出生成：
- 对最终输出进行归一化和线性变换，生成 logits。

总结：

class Transformer 实现了完整的 Transformer 模型，包括嵌入、位置编码、多层 Transformer 块的处理以及最终的输出生成。

示例解析

示例输入

假设我们有以下输入：

输入 tokens: [[1, 2, 3]]，形状为 (batch_size=1, seq_len=3)。
模型参数:
- dim=4（模型维度）。
- n_heads=2（注意力头数）。
- vocab_size=10（词汇表大小）。
- max_seq_len=8（最大序列长度）。

执行流程

1. Token Embedding

输入: tokens = [[1, 2, 3]]，形状为 (1, 3)。
操作: 将 token IDs 转换为嵌入向量。
输出: 嵌入向量，形状为 (1, 3, 4)。

# 假设嵌入矩阵为：
embedding_matrix = [
    [0.1, 0.2, 0.3, 0.4],  # token 1
    [0.5, 0.6, 0.7, 0.8],  # token 2
    [0.9, 1.0, 1.1, 1.2],  # token 3
]
# 输出：
h = [
    [[0.1, 0.2, 0.3, 0.4],  # token 1
     [0.5, 0.6, 0.7, 0.8],  # token 2
     [0.9, 1.0, 1.1, 1.2]]  # token 3
]

2. 添加位置编码

输入: 嵌入向量 h，形状为 (1, 3, 4)。
操作: 使用 freqs_cis 添加旋转位置编码。
输出: 添加位置编码后的向量，形状为 (1, 3, 4)。

# 假设 freqs_cis 为：
freqs_cis = [
    [1.0, 1.0],  # 位置 1
    [1.1, 1.1],  # 位置 2
    [1.2, 1.2],  # 位置 3
]
# 输出：
h_with_pos = [
    [[0.1, 0.2, 1.0, 1.0],  # token 1
     [0.5, 0.6, 1.1, 1.1],  # token 2
     [0.9, 1.0, 1.2, 1.2]]  # token 3
]

3. 初始化 mask

输入: 序列长度 seq_len=3。
操作: 生成注意力掩码，防止模型看到未来的 token。
输出: 注意力掩码，形状为 (3, 3)。

# 输出：
mask = [
    [0, -inf, -inf],  # 位置 1
    [0, 0, -inf],     # 位置 2
    [0, 0, 0]         # 位置 3
]

4. 进入 Transformer 层

输入: 添加位置编码后的向量 h_with_pos，形状为 (1, 3, 4)。
操作: 通过多层 Transformer 块处理输入。

5. Transformer Block 1

输入: h_with_pos，形状为 (1, 3, 4)。
操作:
1. RMSNorm: 对输入进行归一化。
2. Attention: 计算多头注意力机制。
3. Add & Norm: 残差连接和归一化。
4. FeedForward: 计算前馈网络。
5. Add & Norm: 残差连接和归一化。
输出: Transformer 块的输出，形状为 (1, 3, 4)。

# 假设输出为：
h_block1 = [
    [[0.2, 0.3, 1.1, 1.1],  # token 1
     [0.6, 0.7, 1.2, 1.2],  # token 2
     [1.0, 1.1, 1.3, 1.3]]  # token 3
]

6. Transformer Block N

输入: 上一层的输出，形状为 (1, 3, 4)。
操作: 重复 Transformer 块的处理。
输出: 最后一层 Transformer 块的输出，形状为 (1, 3, 4)。

# 假设输出为：
h_blockN = [
    [[0.3, 0.4, 1.2, 1.2],  # token 1
     [0.7, 0.8, 1.3, 1.3],  # token 2
     [1.1, 1.2, 1.4, 1.4]]  # token 3
]

7. RMSNorm

输入: 最后一层 Transformer 块的输出，形状为 (1, 3, 4)。
操作: 对输出进行归一化。
输出: 归一化后的输出，形状为 (1, 3, 4)。

# 假设输出为：
h_norm = [
    [[0.4, 0.5, 1.3, 1.3],  # token 1
     [0.8, 0.9, 1.4, 1.4],  # token 2
     [1.2, 1.3, 1.5, 1.5]]  # token 3
]

8. 输出线性变换

输入: 归一化后的输出，形状为 (1, 3, 4)。
操作: 通过线性层将输出映射到词汇表空间。
输出: logits，形状为 (1, 3, vocab_size=10)。

# 假设输出为：
logits = [
    [[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],  # token 1
     [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1],  # token 2
     [0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2]]  # token 3
]

最终输出

输出: logits，形状为 (1, 3, 10)。
解释: 每个 token 的输出是一个长度为 vocab_size=10 的向量，表示每个 token 的概率分布。

总结

输入: tokens = [[1, 2, 3]]，形状为 (1, 3)。
输出: logits，形状为 (1, 3, 10)。
中间步骤:
1. Token Embedding：(1, 3) -> (1, 3, 4)。
2. 添加位置编码：(1, 3, 4) -> (1, 3, 4)。
3. 初始化 mask：(3, 3)。
4. 多层 Transformer 块：(1, 3, 4) -> (1, 3, 4)。
5. RMSNorm：(1, 3, 4) -> (1, 3, 4)。
6. 输出线性变换：(1, 3, 4) -> (1, 3, 10)。

文章合集：chongzicbo/ReadWriteThink: 博学而笃志，切问而近思 (github.com)

个人博客：程博仕

微信公众号：

微信公众号

人工智能 > nlp > llm

#nlp #llm #llama #源码解析

llama3源码解析-03：model.py模块解析

https://chongzicbo.github.io/2024/12/30/人工智能/nlp/llm/源码解析：llama3源码解析-03：model.py模块解析/

Author

程博

Posted on

December 30, 2024

Licensed under

HTTP基础01：HTTP协议概述 Previous

llama3源码解析-04：generation.py模块解析 Next

llama3源码解析-03：model.py模块解析

整体

1. 模型参数定义 (ModelArgs 类)

2. RMSNorm 层 (RMSNorm 类)

3. RoPE (Rotary Positional Embedding)

4. 注意力机制 (Attention 类)

5. 前馈网络 (FeedForward 类)

6. Transformer 块 (TransformerBlock 类)

7. Transformer 模型 (Transformer 类)

8. 模型并行化

9. 推理模式

总结：

模型详细流程图

class ModelArgs

class RMSNorm

解释：

旋转位置编码

precompute_freqs_cis

解释：

reshape_for_broadcast

解释：

apply_rotary_emb

解释：

总结：

repeat_kv

解释：

class Attention

主要功能：

关键组件：

`流程图

详细步骤说明：

代码实现的关键点：

总结：

FeedForward

详细步骤说明：

代码实现的关键点：

总结：

TransformerBlock

详细步骤说明：

代码实现的关键点：

总结：

class Transformer

详细步骤说明：

整体流程：

Transformer Block 子流程：

代码实现的关键点：

总结：

示例解析

示例输入

执行流程

1. Token Embedding

2. 添加位置编码

3. 初始化 mask

4. 进入 Transformer 层

5. Transformer Block 1

6. Transformer Block N

7. RMSNorm

8. 输出线性变换

最终输出

总结

1. 模型参数定义 (`ModelArgs` 类)

2. RMSNorm 层 (`RMSNorm` 类)

4. 注意力机制 (`Attention` 类)

5. 前馈网络 (`FeedForward` 类)

6. Transformer 块 (`TransformerBlock` 类)

7. Transformer 模型 (`Transformer` 类)

`class ModelArgs`

`class RMSNorm`

`precompute_freqs_cis`

`reshape_for_broadcast`

`apply_rotary_emb`

`repeat_kv`

`class Attention`

`FeedForward`

`TransformerBlock`

`class Transformer`